Researcher: Ferdia Sherry, Erlend Riis, Luca Calatroni, and Carola-Bibiane Schönlieb
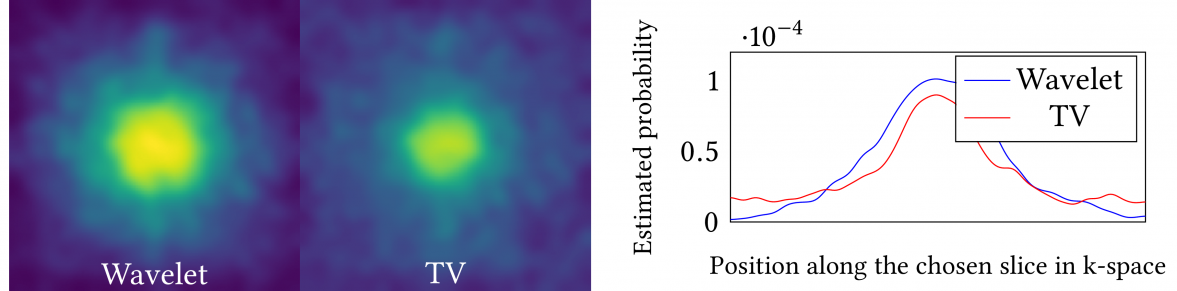
The discovery of the theory of compressed sensing brought the realisation that many inverse problems can be solved satisfactorily even when measurements are "incomplete". This is particularly interesting in magnetic resonance imaging (MRI), where long acquisition times can limit its use. The measurements taken in MRI are usually modelled as samples of the Fourier transform of the signal to be recovered. In this work, we consider the problem of learning a sparse sampling pattern to obtain high quality reconstructions. We use a supervised learning approach to this problem and naturally come to a bilevel optimisation problem that is solved to learn the sampling pattern. The proposed framework is general enough to learn arbitrary sampling patterns, including common patterns such as cartesian, spiral and radial sampling.
