Multiplying binary numbers

Two input images are created such that 2x4 patch in left image and 2x4 patch in corresponding region of right image represent two numbers (x and y) in binary format. The binary number is ordered on a row by row basis within the 2x4 patch with bit 0 (lsb) in the top left hand corner and bit 8 (msb) in the bottom right hand corner of the image patch. The product of these two numbers, z = x*y, varies in a smooth fashion across the surface of the image. z is initially chosen in the range [0,1] and then scaled by 2**15. Given z, we chose x to be a random value between 1 and 255, and then we set y = z/x. (If y is bigger than 255 then we chose another random value for x until a value for y in the range [1,255] is found.) To ensure that there is no bias in the values of x and y through this selection procedure, the values of x and y are swapped with probability 0.5.

A three-layer network was used, with 2x4x2 inputs going to a hidden layer of 3 tanh units and 1 output unit. Half-lives for averaging: U=5, V=500.

The inputs to the network are the following two binary images (no smoothing or normalisation of input patches):

The product of the two patches in each image has an "egg-box" profile (shown on the left). Network performance after 200 epochs is shown on the right. Final correlation between desired and actual output is -0.994.

Value of merit function and correlation during learning

[All images here are jpegs which accounts for the poor quality on some of the graphs.]

Note this is a very low value of the merit function -- typically we used to see values of around 1.8 for the disparity test and around 0.9 for the feature orientation. [It is negative since we are taking logs and the value V/U has gone below 1.0.]

Testing on unseen data

To test that the network is computing the sum, a new pair of images were created, this time with the sum of the inputs varying in a Gaussian fashion across the two images.

Inputs are just the binary values (no smoothing or normalisation of input patches):

The product of the two patches in each image has a Gaussian profile (shown on the left). Network performance using the network trained on egg box data above is shown the right. Correlation between the two is -0.977, hence the network has generalised from the egg-box data to the gaussian data.

The network was also tested on another pair of inputs where z varied randomly over the image (inputs not shown). Correlation between the desired output (below left) and network output (below right) was -0.995.

In this case, the merit function reached a stable value of -0.8 after around just 10 epochs. When tested on the unseen Gaussian images, correlation was very high (-0.97).

The weights

Here we show the weights for the 3 layer network with 5 hidden units.

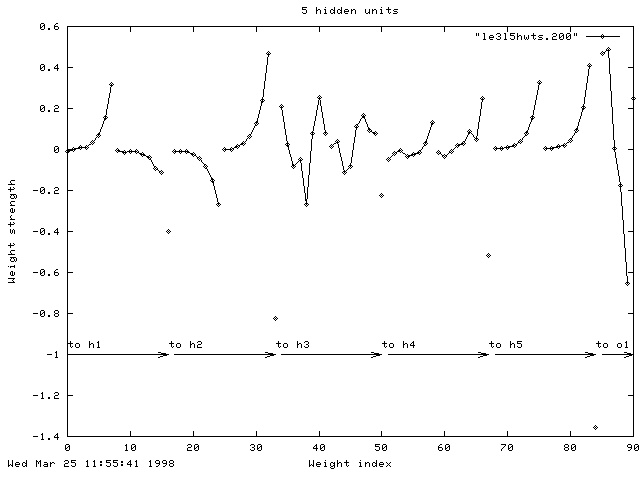
For each of the five hidden units (h1...h5) you see the connections to the eight inputs from the left patch, then the eight inputs from the right patch and then the bias unit. For the connections to the output unit (o1) you see the weights from the five hidden units and then the bias weight. The weights to the third hidden unit look quite strange, although the strength of the connection from h3 to o1 is almost zero so that unit is probably not being used.

The network was also tested with three, rather than five, hidden units. Although the final correlation at the end of learning was high (0.972), it didn't generalise across to the test images very well (When tested on Gaussian data, r=0.800. However, when tested on the random data, r maintained a high value of 0.976).

Two layer nets

To see if the network could learn without a hidden layer, another network was set up with 2x4x2 inputs and one tanh output unit. The short-range half life was varied between 1 and 6, but the network failed to learn the egg-box data:

Half-life 1. r = 0.375

Half-life 3. r = -0.374

Half-life 5. r = -0.462

Half-life 6. r = -0.491

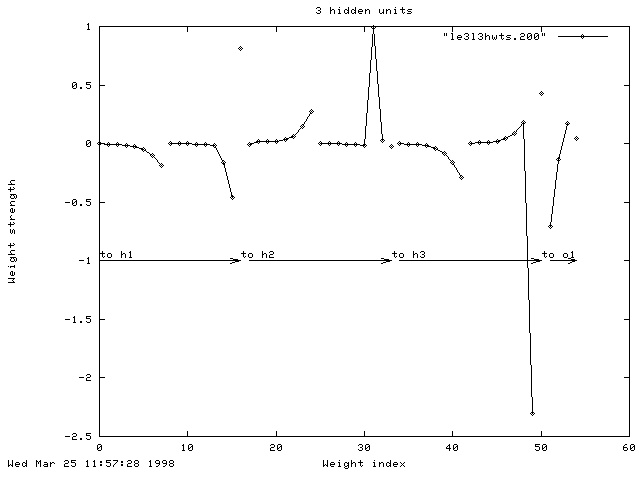
See also adding numbers.