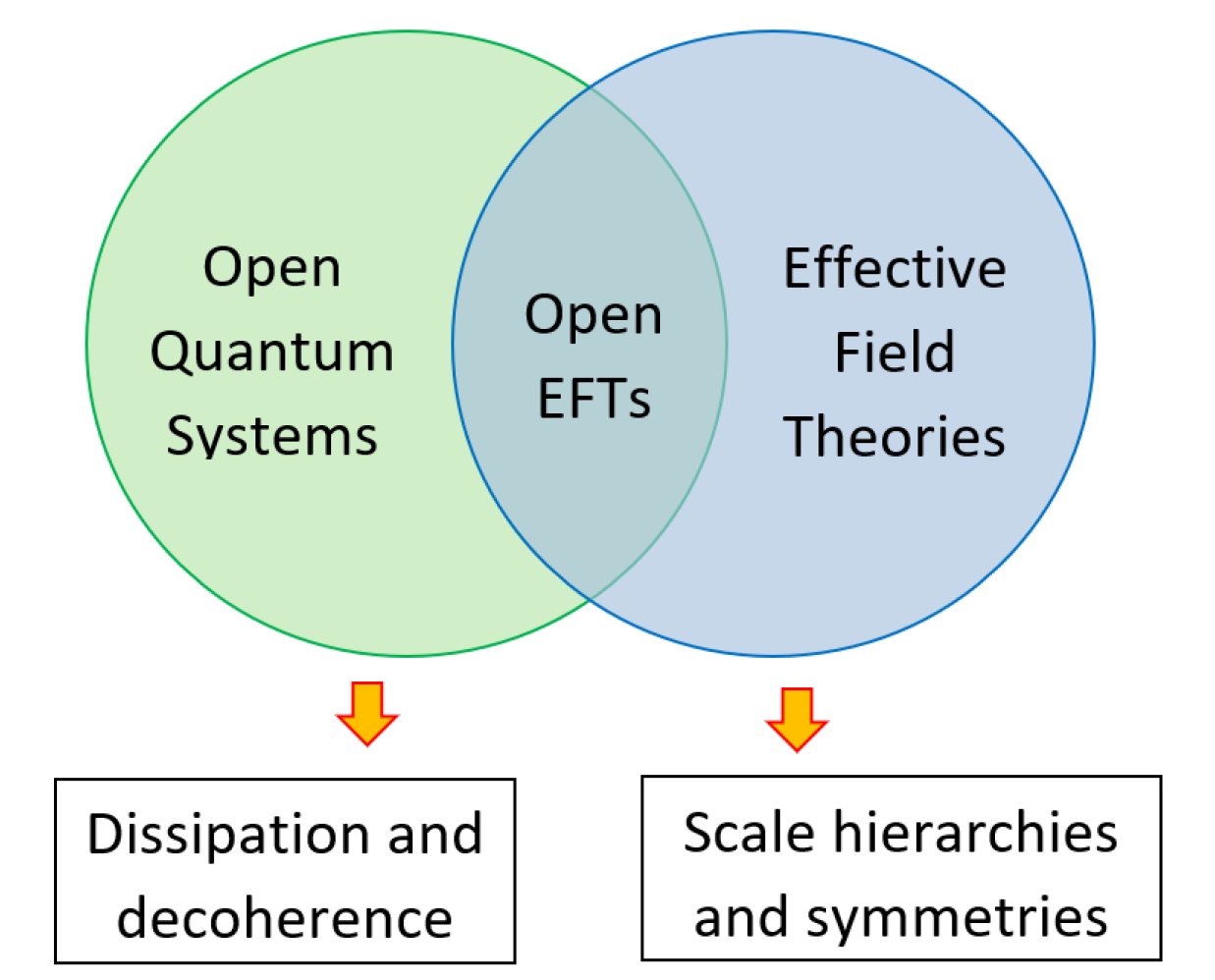
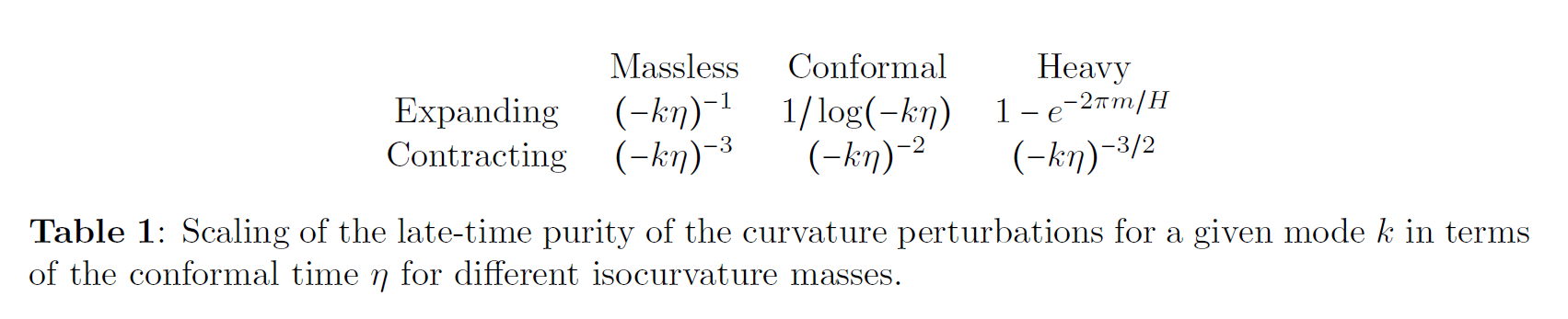When I was a master student, I discovered the fascinating world of Effective Field Theories (EFTs) working with Leonardo Senatore on cosmological Large Scale Structures. EFTs exploit symmetries and scale hierarchies to encode unknown physics in a systematic and controlled manner. EFTs enriched my vision of physics: if I cannot know everything, I will at least try to parametrize my ignorance.


Some years later, I started a PhD in Paris with Vincent Vennin and Julien Grain on the original question that brings me to study physics: cosmic inflation. How can tiny quantum fluctuations in the very early universe seed structure formation of galaxies, clusters and filaments in the late universe? Among the many issues inflation raises, I especially wanted to understand if we can observationally prove the quantum origin of cosmic inhomogeneities.


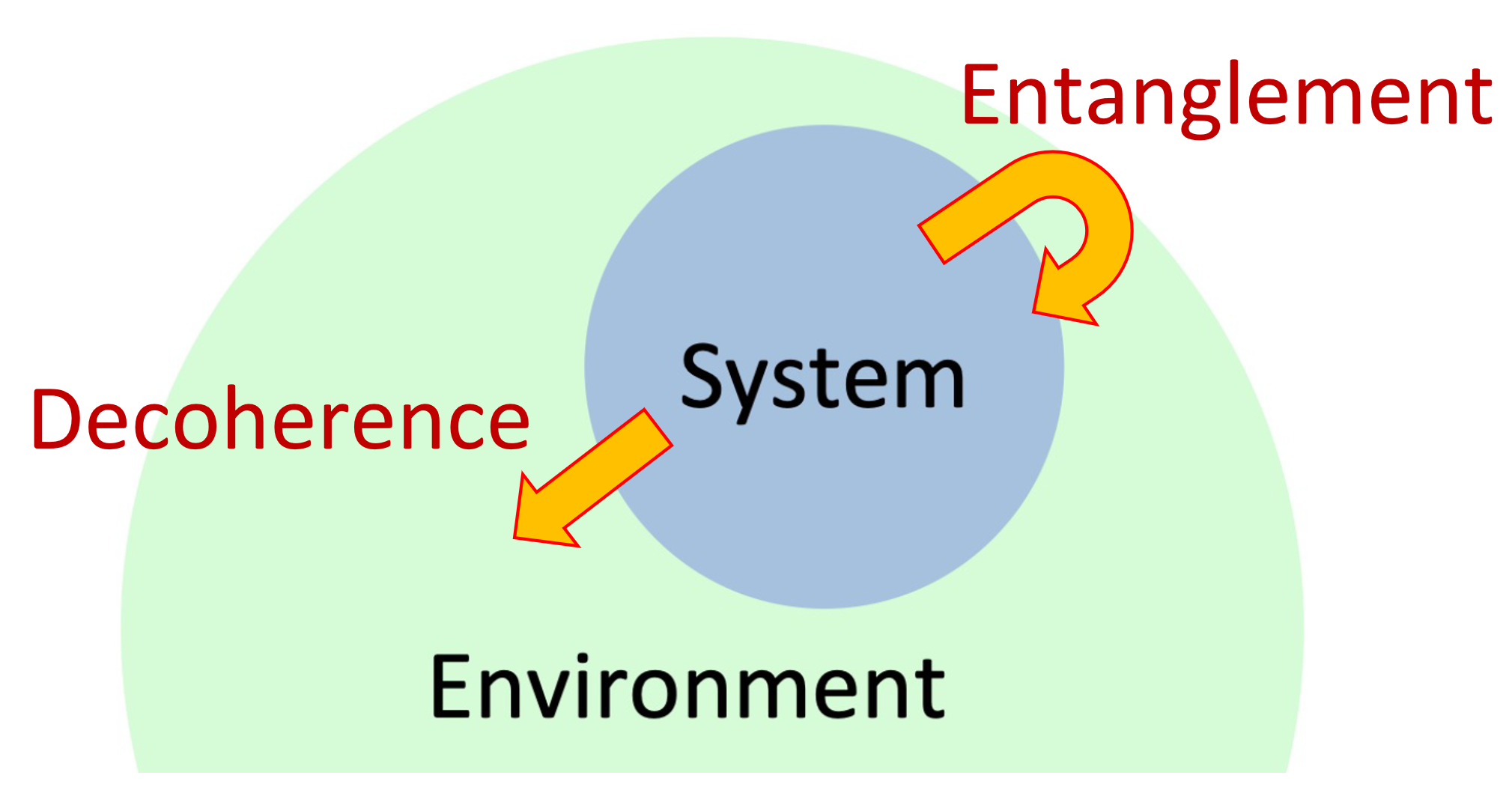
It led me to consider how do we prove that something is quantum, or alternatively why do we sometimes perceive things as being classical. When quantum systems interact with unobservable environments, leakages of information wash away quantum features after very short timescales through quantum decoherence. It explains why quantum features are so fragile. In the presence of unobserved sectors in the early universe, decoherence is a major obstruction to the observation of genuine quantum features. And in fact, we only observe a very tiny subset of all the information contained within the early universe by accessing the summary statistics of curvature perturbations on large scales. (Credit: https://arxiv.org/abs/quant-ph/0306072)


This urges the need for techniques able to model the impact of unobserved sectors on observable cosmology which led to the development of Open Quantum Systems (OQS) in cosmology. OQS are mostly used in quantum optics and condensed matter to account for the eventual leakage of energy and information from the experimental system to its surrounding environment. I spent a lot of time and energy working on developing and benchmarking cosmological OQS to account for the presence of unknown environment in the early universe.

Ultimately, the question behind is the same as for EFTs: How do we encode the impact of unkown physics on observable sectors? Yet, the comparison often stops here: EFTs and OQS do not rely on the same approximations, do not aim at computing the same observables, do not use the same formalisms and do not describe the same physics. In particular, EFTs often aim at writing down a local effective action while OQS are taylored to account for non-Hamiltonian evolutions related to dissipative and diffusive effects.

The development of non-equilibrium EFTs (see https://arxiv.org/abs/1805.09331 for a review) in the last 10 years bridges this gap. Exploiting the versatility of the Schwinger-Keldysh formalism, it proposes a path-integral formulation of the dissipative hydrodynamics. This provides a unified framework to embrace both the usual EFT constructions and the inclusion of dissipative and diffusive effects studied in OQS. In particular, this is the approach we followed to construct the Open EFT of Inflation. Many thanks to those who accompanied and guided me in this journey, I’m looking forward what’s coming next.

One of the most striking predictions of the standard model of cosmology is to trace back the origin of cosmic inhomogeneities to quantum fluctuations of the primordial vacuum. This feature makes cosmology an interesting playground to test quantum mechanics in its most extreme regimes. Yet, such an ambitious program requires an accurate description of the quantum history of the universe. At the moment, an exact description seems out-of-reach as the early universe physics remains elusive on the precise number of degrees of freedom acting during inflation and their fundamental properties (mass, spin). My work aims at providing a quantum description able to incorporate our uncertainties on the exact modelling of the early universe.

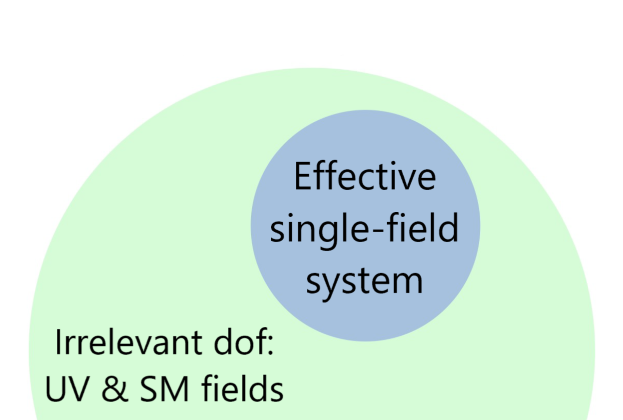Nearly scale-invariant, Gaussian and adiabatic scalar perturbations from quantum mechanical origin have been extensively tested using Cosmic Microwave Background (CMB) and Large Scale Structures (LSS) data. Effective field theories (EFT) aim at providing a systematic way to consider extensions to this adiabatic evolution, incorporating the knowledge of unknown physics in a parametrically controlled manner. In order to grasp the implications of some hidden sector at the quantum level, the formalism needs to incorporate non-unitary effects such as dissipation and decoherence. To achieve this goal, Open Quantum Systems (OQS) Theory may be a valuable tool. Ubiquitous in quantum optics where it describes the effects of an almost unspecified environment on the evolution of measurable degrees of freedom, its implementation often relies on assumptions that do not straightforwardly extend to cosmology where the background is curved and dynamical, the Hamiltonian time-dependent and the environment out-of-equilibrium. Most of my PhD have been devoted to understand how can we construct Cosmological Open Quantum Systems.

In this article, we construct a general open EFT describing local dissipative models of inflation. Based on the seminal work of https://arxiv.org/abs/1109.4192, we describe the Goldstone boson of time-translations interacting with an unknown environment. The understanding of symmetries in non-equilibrium and open systems developed in https://arxiv.org/abs/1805.06240 and https://arxiv.org/abs/2306.17232 is crucial to the construction. Locality emerging from a hierarchy of scale is also a limiting yet necessary assumption to ensure the existence of a truncatable power counting scheme.

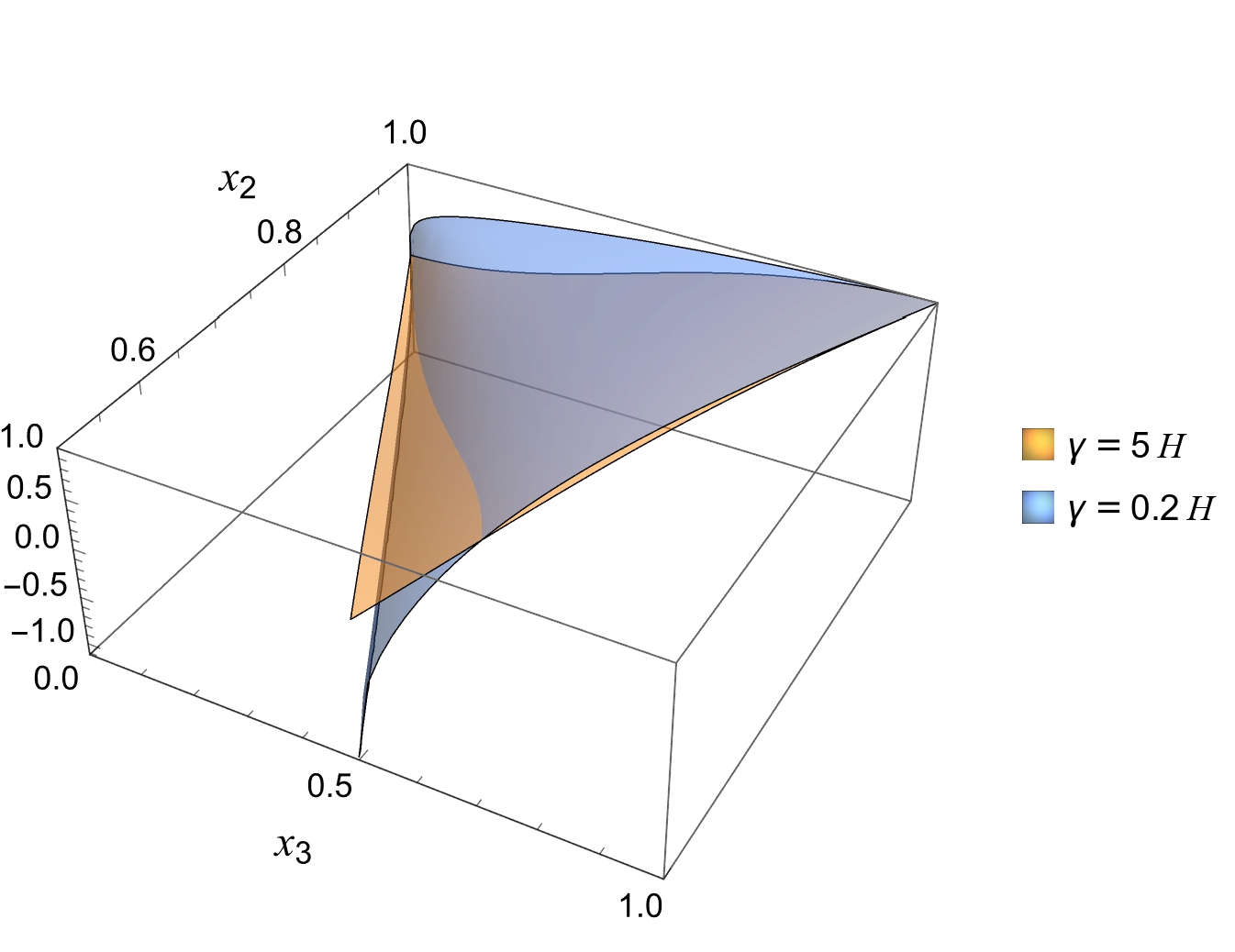
Under these assumptions, we derived the power spectrum and bispectrum associated to this class of models which can be compared to the CMB and LSS data. It has some b>specific features, such as an enhanced but finite bispectrum near the folded region in the low dissipation regime (blue region in Figure).

This generic construction can be matched to specific models of local dissipative inflation as the one of https://arxiv.org/abs/2305.07695.

This work opens many questions. What are the phenomenological consequences of allowing for dissipative and diffusive effects in cosmological EFTs? Beyond inflation, can it impact our understanding of the late-time acceleration of the universe? Can we exploit entropy measures and quantum information properties to better understand quantum field theory in curved-spacetime?

Electromagnetism in a medium is a century-old problem, yet understanding gauge symmetries in Open Effective Field Theories remains challenging. Sometimes, it's helpful to take a step back. In cosmology, we aim to compare the observed statistics of galaxies in the sky with theoretical predictions, known as cosmological correlators


These correlators are computed using the principles of finite-time QFT. Instead of the usual path integral used in particle physics, we work with the Schwinger-Keldysh contour, which looks like this:


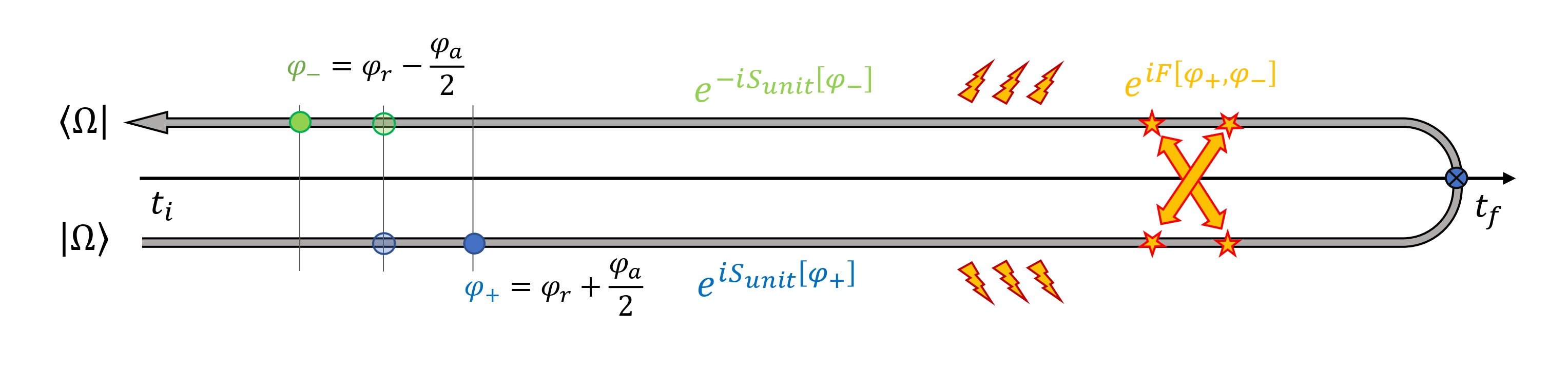
One of the key innovations this contour introduces is the ability to encode dissipation and noise through the mixing of the branches in the path integral. Understanding how physical principles, such as symmetries and locality, constrain these effects is especially important in situations where they naturally emerge, such as in cosmology.

As a step toward dynamical gravity, we first studied Abelian gauge theories. While formal approaches to this problem are well-established (see, e.g., https://arxiv.org/abs/2306.17232), our focus here is on a practical implementation. In our article, we construct the most general open effective field theory for electromagnetism in a medium, describing photons that experience dissipative effects and environmental noise. Our main observation is that the two copies of the gauge group, one for each branch of the path integral, are not broken but rather deformed by dissipative effects.

The main consequence of the deformed gauge invariance is a constraint on the matter current and the noise sourcing the E&M sector. It appears that the current perceived by the photon is not conserved in the presence of dissipation. However, the deformed gauge invariance provides sufficient structure to ensure that only two physical degrees of freedom remain. Ultimately, our construction encapsulates the well-known properties of media that are diffusive (refractive index), dispersive (dissipation), anisotropic (birefringence), and imperfect (impurities).

I now feel more confident when discussing stochastic QFT and its extensions to Open EFTs. Hopefully, this clears one more obstacle toward applying these techniques to dynamical gravity. Next targets: dark energy and gravitational waves!

In cosmology, we often calculate the statistics of fluctuations we observe in the sky: mean, variance, skewness, kurtosis, etc. These quantities, known as cosmological correlators, provide information about the universe's content at a specific time.

In quantum information theory, we define a bipartition and seek to characterize the amount of information shared between the two parts. To achieve this, we compute entropy measures such as purity and entanglement entropy. 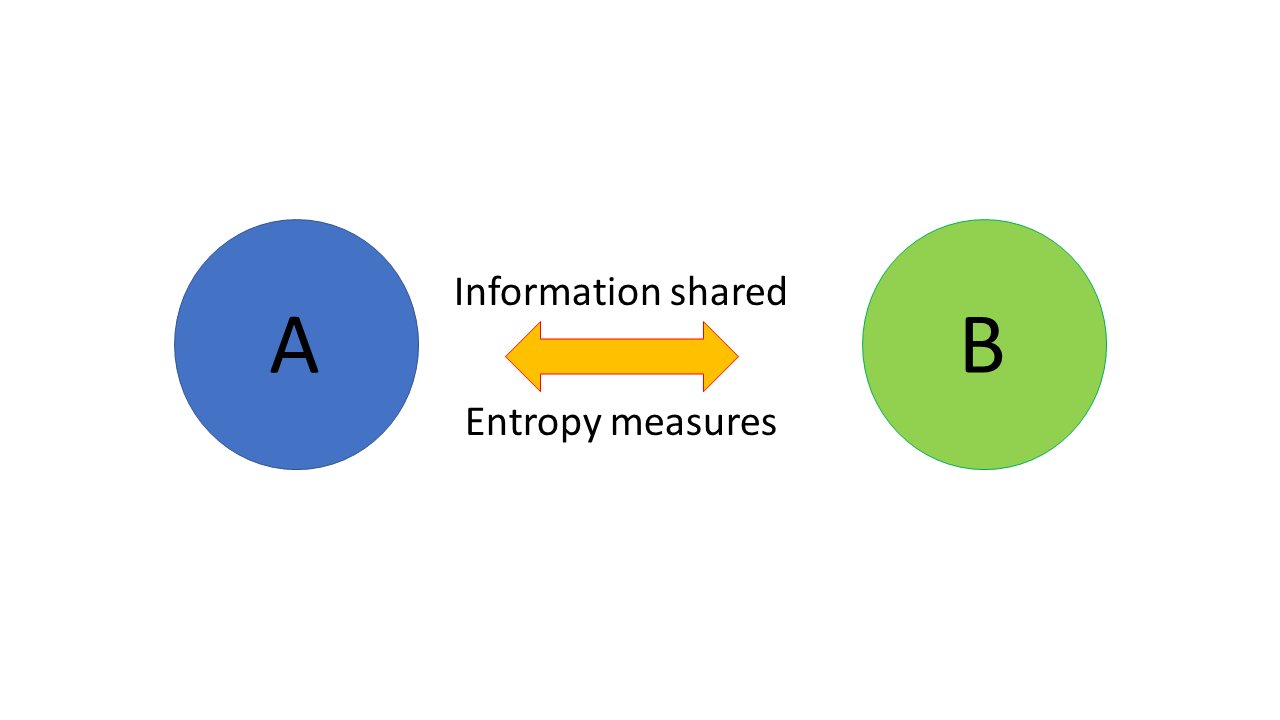The goal of our article is to adapt the perturbative framework known as the in-in formalism, usually used to compute cosmological correlators, to the evaluation of entropy measures of quantum fields in curved spacetime. The bipartition we considered is made of two quantum fields with different quantum numbers (mass, spin, charges, etc.). We expand in the coupling constant of the interaction Hamiltonian entangling these two sectors.

We derive Feynman rules to compute the purity (the simplest of these entropy measures). It generates diagrams like this where blobs represent unequal-time correlators of the two fields. Applied to specific models, it allows us to single out the contributions we need to compute.


For Gaussian systems, the two-point functions characterise the entropy measures. We show that, at leading order, this remains true for non-Gaussian states if one considers non-linearities quadratic in the system. Can we go beyond this result by considering higher order statistics?

Now that the problem is framed in terms of (equal or unequal-time) correlators, one could investigate the role of symmetries, UV unitarity and locality in the evolution of the quantum information properties of the system. An exciting program on the horizon!

In this Letter, we discover a mechanism of quantum recoherence for the adiabatic perturbations when they couple to an entropic sector.


Despite being created through a fundamentally quantum-mechanical process, cosmological structures have not yet revealed any sign of genuine quantum correlations. Among the obstructions to the direct detection of quantum signatures in cosmology, quantum decoherence is arguably one of the most inevitable. If a system exhibits quantum correlations that we may reveal by performing a Bell test, interactions with a surrounding environment has tendency to wash away any hope of observing non-classical features. Information is delocalised into the environment which we cannot experimentally access and we lose chances to exhibit quantumness. 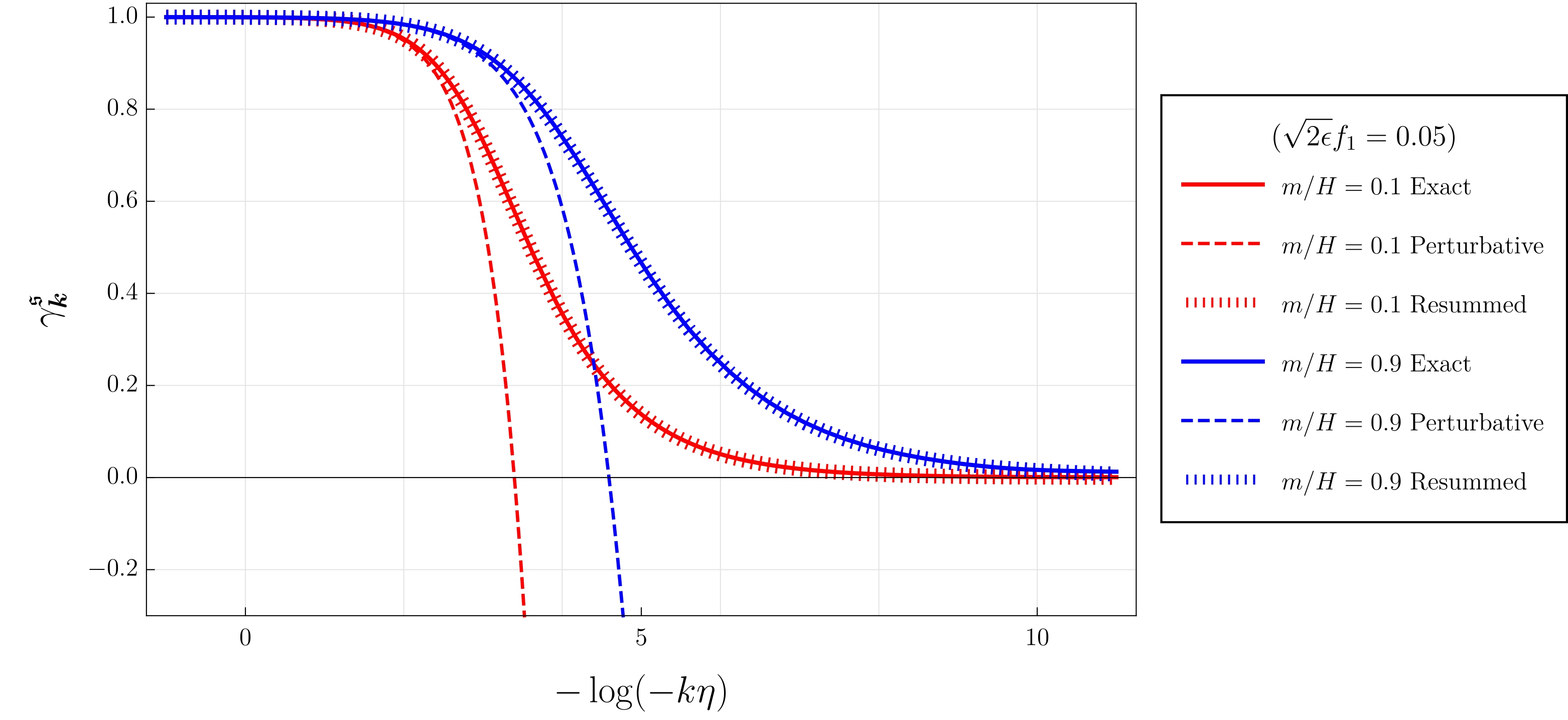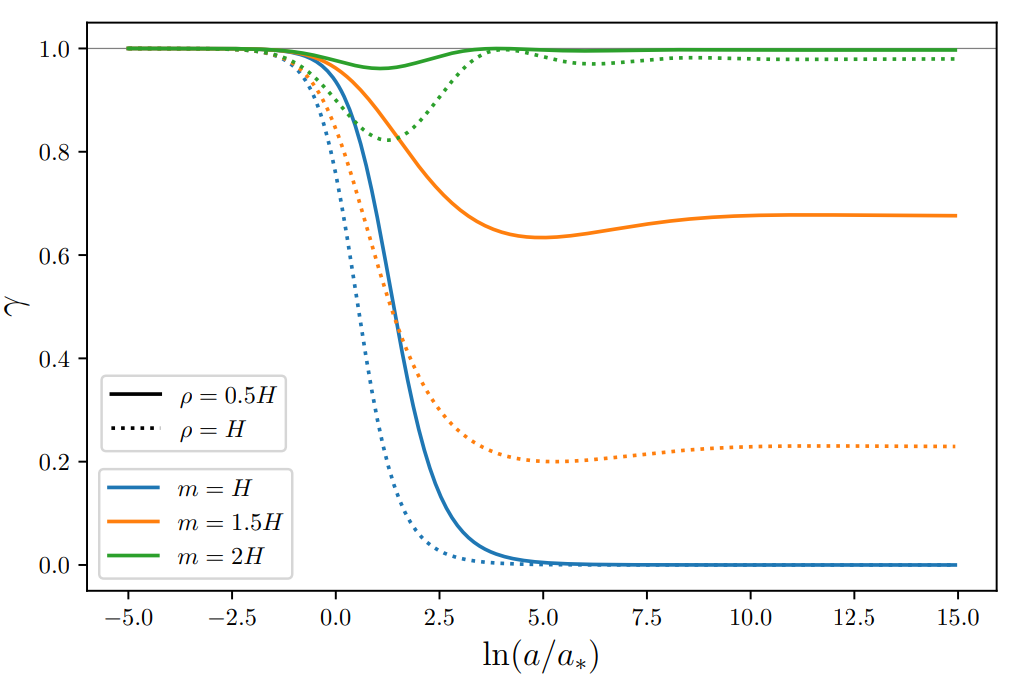We track this phenomenon thanks to an object called the state purity, plotted above as a function of the number of efolds for a given mode during inflation. If the purity is close to one, one may hope to exhibit non-classical correlations if there is any. On the contrary, when the purity is close to zero, the state is mixed and it can be reproduced by a classical statistical distribution.

In primordial cosmology, decoherence is often invoked to explain why the universe looks so classical. It has been studied for various cosmological environments, for instance made of the unobservable short wavelength modes . We typically expect the purity to fall to zero shortly after Hubble crossing. In our new paper, we investigated another type of environments made of a heavy scalar extension to single-field slow roll inflation. The Lagrangian of the perturbations captures the leading effect in the derivative expansion of generic multiple-field models. Contrary to common wisdom, we discover that, after a transient phase of decoherence, recoherence takes place and the final state exhibits large levels of self-coherence. Heavy entropic degrees of freedom do not lead to quantum decoherence of adiabatic fluctuations in the early universe, at least through their dominant interaction term. We finally observe that at one can either obtains recoherence (m > 3H/2), purity freezing (m ~ 3H/2) or decoherence (m < 3H/2), depending on the mass of the entropic degree of freedom.


To gain some insight, we also derive an effective single-field open description using a non-Markovian master equation. It contains a unitary part which reproduces the Wilsonian EFT results supplemented by a non-unitary contribution which captures the recoherence phenomenon. These results do not preclude other decoherence channels (such as higher-order coupling between adiabatic and entropic fluctuations, single-field gravitational decoherence, etc.) to effectively decohere cosmological perturbations, but it suggests that decoherence in the early universe may not be as ubiquitous as common wisdom suggests. Most importantly, it highlights how quantum dynamics in cosmology can depart from their flat spacetime analogues. This invites us to critically assess the applicability of Open Quantum System tools in cosmology.

How does the decoupling of low energy degrees of freedom from high energy physics happen in flat space QFT? We investigate this question with C.P. Burgess, R. Holman and G. Kaplanek in this article through the use of entropy measures.

We consider two scalars with a large mass hierarchy m << M, initially set up in a vacuum state. Using Schwinger-Keldysh techniques, we trace over the heavy field and observe entropy measures such as the purity receive 1/M corrections. These corrections cannot be captured by a local and self-adjoint Hamiltonian. Physically, they correspond to a change in the occupation number of the light field which is displaced from its initial vacuum. By performing a late-time i-epsilon prescription, we guarantee the system remains in its vacuum throughout the dynamical evolution. We recover the decoupling expectation that all 1/M effects are captured by a local Hamiltonian

In the end, expectations of decoherence or decoupling depend on the relation between the heavy mass M and the EFT cutoff ?. When M << ?, finite size effects of order 1/M can affect entropy measures. On the contrary, when M >> ?, these effects remain below the resolution threshold and the effective evolution is Hamiltonian. We found this exercice useful to understand the articulation between standard in-out computations in which decoupling is ubiquitous and their extension to in-in contours where new effects such as decoherence and thermalization occur.

I hope this work will foster the dialogue between physicists that may have different expectations regarding decoherence and decoupling!

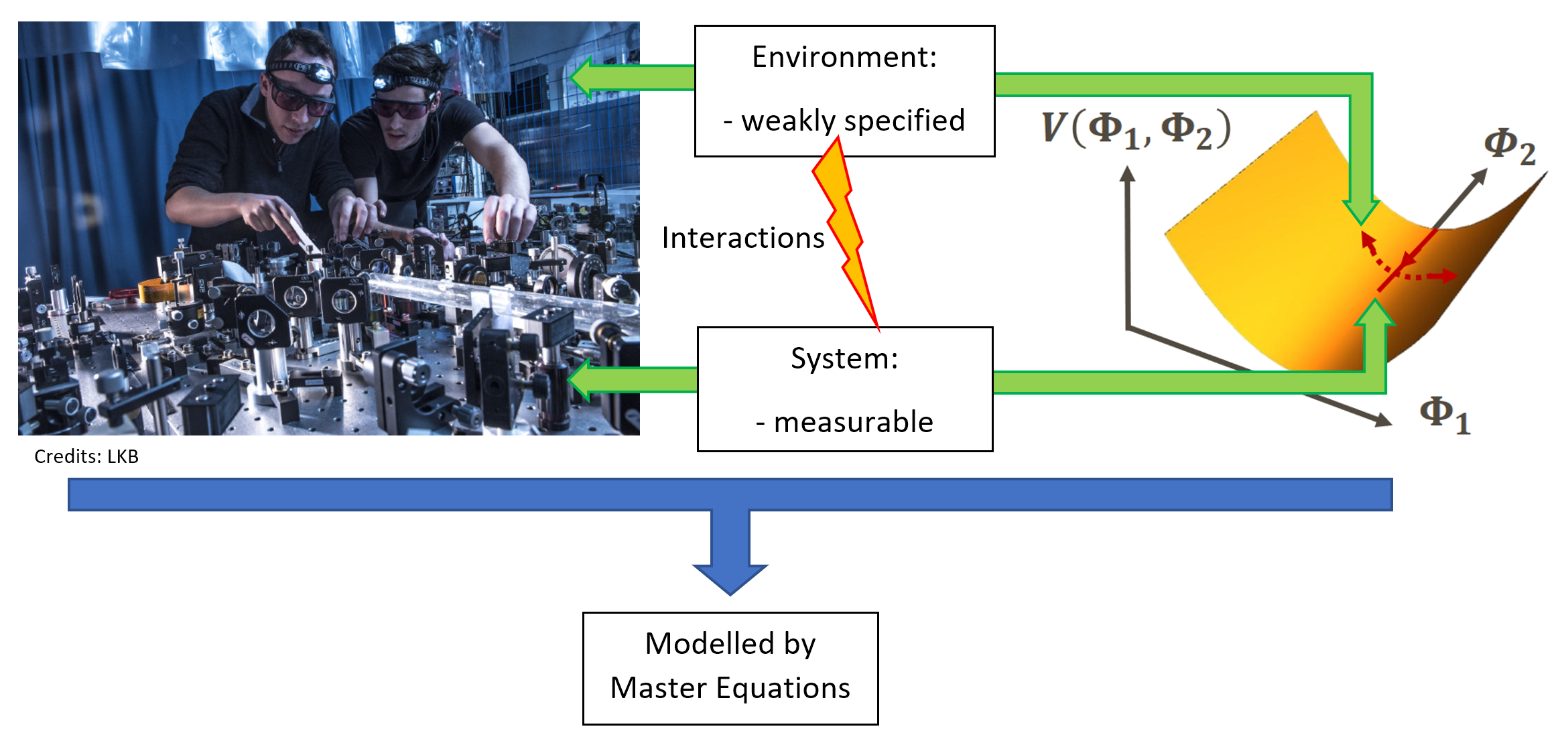Master equations are commonly employed in cosmology to model the effect of additional degrees of freedom, treated as an environment, onto a given system. However, they rely on assumptions that are not necessarily satisfied in cosmology, where the environment may be out-of-equilibrium and the background is dynamical. For this reason, we applied the master-equation program to a model that is exactly solvable, and which consists of two linearly coupled scalar fields evolving on a cosmological background. The light field plays the role of the system and the heavy field is the environment. By comparing the exact solution to the output of the master equation, we critically assessed its performance.

To perform this work, we had to review the approximations schemes on which relies the master equation program. The most comprehensive approach starts with the rewriting of the exact dynamics focusing on the system degrees of freedom known under the name of Nakajima-Zwanzig (NZ) master equation. One can then perform a systematic expansion in the smallness of the system-environment coupling known under the name of Born approximation. It leads to a local in time non-Markovian master equation, the Time-ConvolutionLess (TCL) master equation, which so far does not rely on any assumption on the nature of the environment itself. Finally, when the environment is made of a large number of interacting degrees of freedom such that it forms a thermal bath, one can proceed one step further and implement the Markov approximation. Indeed, correlations are short lived in a thermal bath so that the environment is not able to keep track of the past interactions with the system. In this case, the system follows a semi-group evolution modelled by a Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) master equation. The chart below provides a summary of the various layers of approximation that lead us from exact (left) to Markovian (right) master equations.


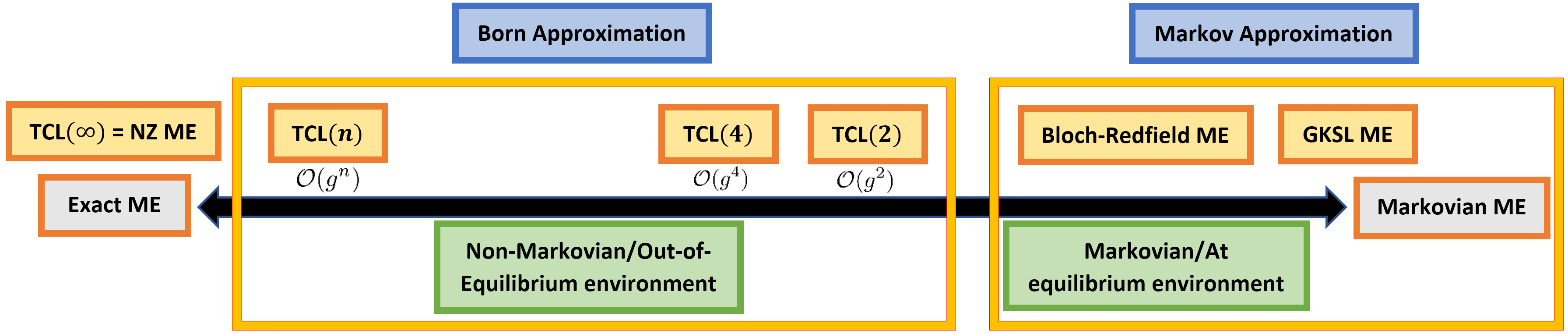
In the exactly solvable model we studied, the environment does not reach thermal equilibrium nor the Markovian limit. Hence, we worked within the non-Markovian framework of the TCL master equations. The environment affect the system in three ways: a unitary Lamb-shift term (renormalisation of the bare Hamiltonian), a damping term (energy dissipation into the environment) and a diffusive term (driving the quantum decoherence process). If we solve the master equation perturbatively, we just recover the standard result of cosmological perturbation theory, that is the so called in-in results. There is a way to perform a meaningful resummation only at the expense of removing by hands a set of terms dubbed as "spurious", which do not exist in the perturbative limit of the theory, and which explicitly depend on the initial conditions. When those terms are removed, the master equation performs impressively well to reproduce the power spectra and the amount of the decoherence of the light field, even in the strongly decohered regime. We conclude that master equations are able to perform late-time resummation, even though the system is far from the Markovian limit, provided spurious contributions are correctly identified and removed.

In our first collaboration with C. de Rham and G. Kaplanek, we study quantum decoherence during inflation and alternatives. We consider a class of two-field models leading to a nearly scale-invariant power spectrum for curvature perturbations compatible with current CMB and LSS constraints which interpolates between expanding (inflation) and contracting (ekpyrosis) scenarios. We want to understand if the presence of an isocurvature mode leads to quantum decoherence of the curvature perturbations.

We find that ekpyrotic universes lead to complete decoherence of the curvature perturbations before the bounce (left panel). This is in stark contrast to the inflationary case, where recoherence has been previously observed (see above) for heavy isocurvature mode (right panel).


To assess decoherence, we study the purity perturbatively and observe that late-time breakdown of perturbation theory often occurs. Instead, we establish a simple yet powerful late-time purity resummation which captures the exact evolution to a remarkable level, while maintaining analytical control.


Our late-time scaling for the purity is summarized in this Table. Our study reveals how cosmological background plays a crucial role in the decoupling of the heavy fields during inflation and alternatives. More generally, it motivates the construction of Open EFTs which incorporate non-unitary effects in cosmology.

Computations of quantum information properties such as the purity often suffer from late-time secular divergences which plague the perturbative computations. They call for resummations techniques which allow us to extract meaningful late-time results.


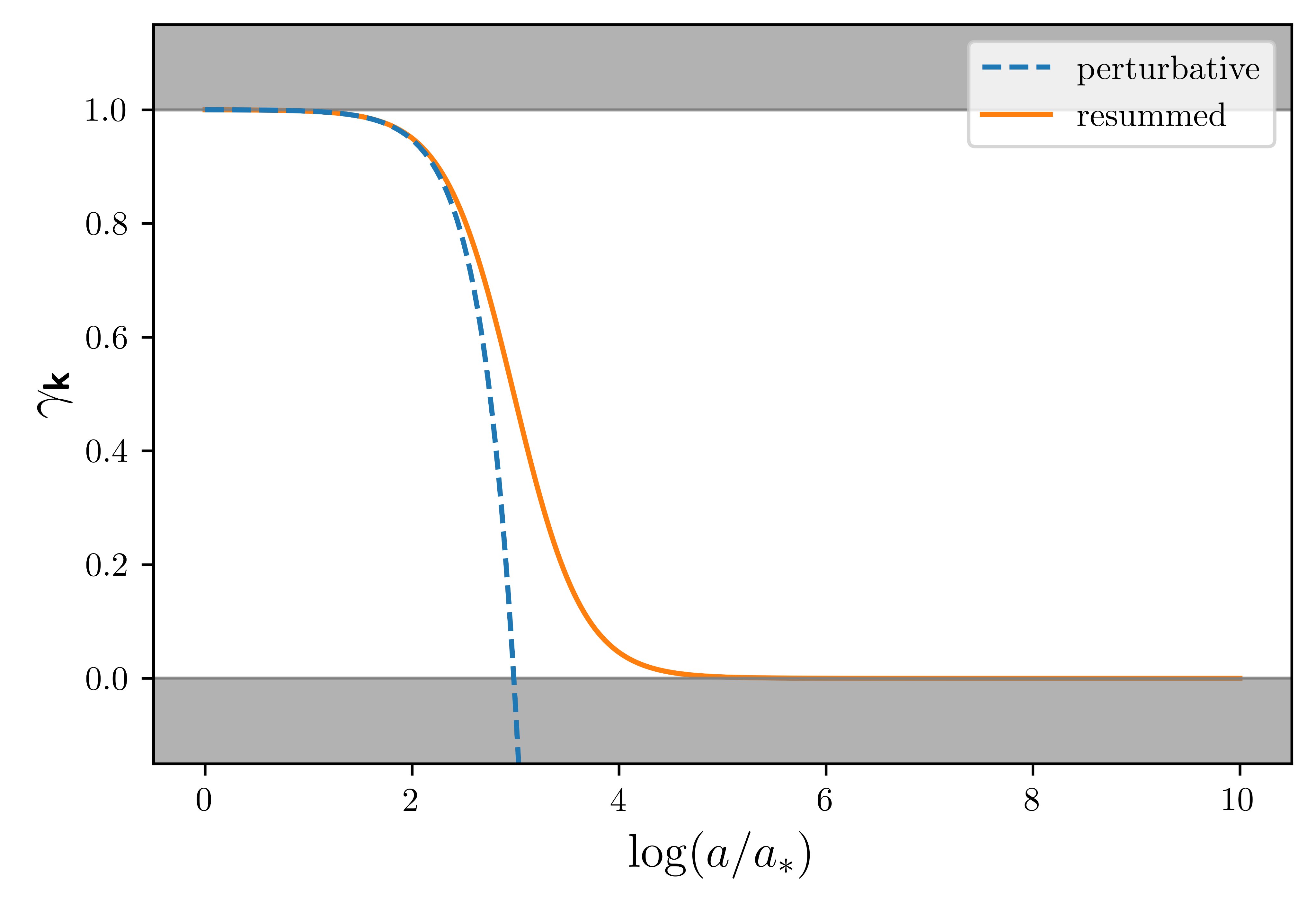
In this Figure, we compare the purity as a function of the number of efolds after Hubble crossing using perturbative (blue) and Open EFTs (orange) techniques. The perturbative breakdown is manifest after a few efolds while the Open EFT result remains valid at late-time.



The existence of a meaningful resummation scheme is not guaranteed per se. In our first collaboration with C. Burgess, R. Holman, G. Kaplanek and V. Vennin, we identify the onset of an underlying Markovian regime on super-Hubble scales which overlaps and supplants the perturbative treatment at late-time.

Homogeneity has tremendous consequences in cosmology, one of which is the fact that at linear order in perturbation theory, excitations can only be created with opposite wavevectors. At the quantum level, it generates a huge amount of entanglement between sectors of opposite momenta known under the name of pair creation process or cosmological Schwinger effect. Indeed, in single-field inflation, cosmological perturbations are placed in a so-called two-mode squeezed state. from which cosmological structures later form. This state exhibit large non-classical features which rise the hope to observationally prove the quantum origin of cosmic structures. Yet, it remains of clarify the amount of entanglement accessible in real space and if genuine quantum signatures are able to stay immune to environmental effects such as quantum decoherence.

For these reasons, we investigated quantum aspects of two-field cosmology. The generalization of the squeezing formalism to two-field cosmology naturally leads to the concept of four-mode squeezed states. These quantum states can be understood as two single fields exchanging quanta. If the pair creation process dominates over the exchange of quanta, large intra-sector entanglement can be reached. This study allows us to investigate this process quantitatively, connecting it to the microphysical properties of the fields (masses, coupling).

Thanks to the many efforts made in understanding the dark sector, an unprecedented volume of data will be collected by the next generation of Large Scale Structures (LSS) surveys such as EUCLID and LSST. Using this information, LSS could potentially beat the Cosmic Microwave Background (CMB) constraints on primordial parameters. Yet, this goal is only reachable if a theory is able to accurately describe the dynamics at small scale, where non-linearities become large.

At short distances, the dark matter dynamics is extremely complicated, dominated by galaxy formation, collisions and even stellar processes. Consequently, modes are coupled at the non-linear level and short-distance physics can backreact on the long-wavelength fluctuations by sequences of uncontrolled non-linear mechanisms. Theoretically, this uncontrolled short-distance feedback appears in perturbation theory through the UV-divergencies of the loop integrals. The Effective Field Theory of the Large Scale Structures (EFTofLSS) introduces a set of Wilson coefficients that allow to systematically renormalize the theory order by order in perturbation theory, parametrizing the effect of the unknown short-distance physics in the most general way.

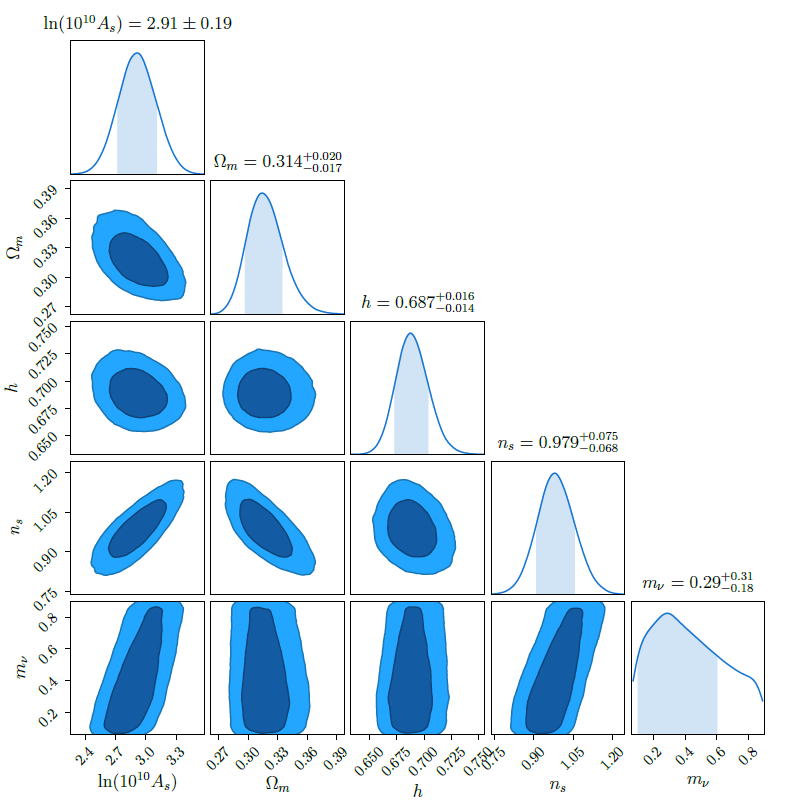In practice, the EFTofLSS is a formalism which allow us to analytically compute the galaxy clustering power spectrum at arbitrary precision in the mildly non-linear regime. By applying this tool to the redshift-space one loop power spectrum, we analyzed the BOSS DR12 data and scanned over all the parameters of LambdaCDM cosmology with massive neutrinos. My own contribution consisted in extending the previously existing pipeline to incorporate three new cosmological parameters that are the abundance of baryons, the tilt of the primordial power spectrum and the sum of neutrino masses.