Dynamics of astrophysical discs
Discs are ubiquitous in astrophysics and participate in some of its most important processes. Most, but not all, feed a central mass: by facilitating the transfer of angular momentum, they permit the accretion of material that would otherwise stay in orbit. As a consequence, discs are essential to star, planet and satellite formation. They also regulate the growth of supermassive black holes and thus indirectly influence galactic structure and the intra-cluster medium. Although astrophysical discs can vary by ten orders of magnitude in size and differ hugely in composition, all share the same basic dynamics and many physical phenomena.
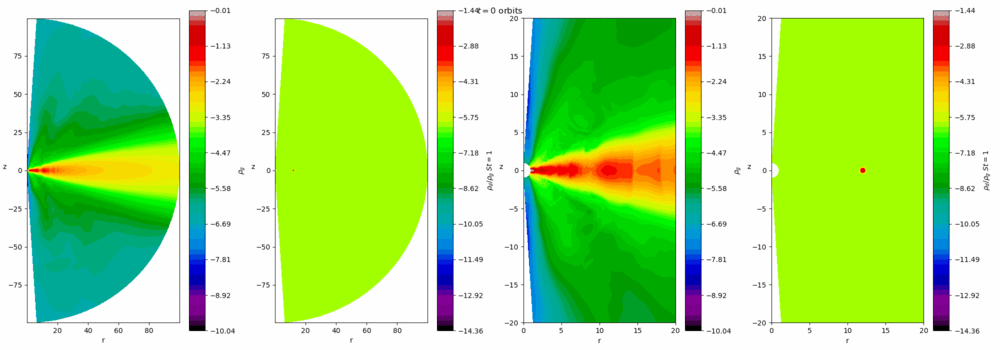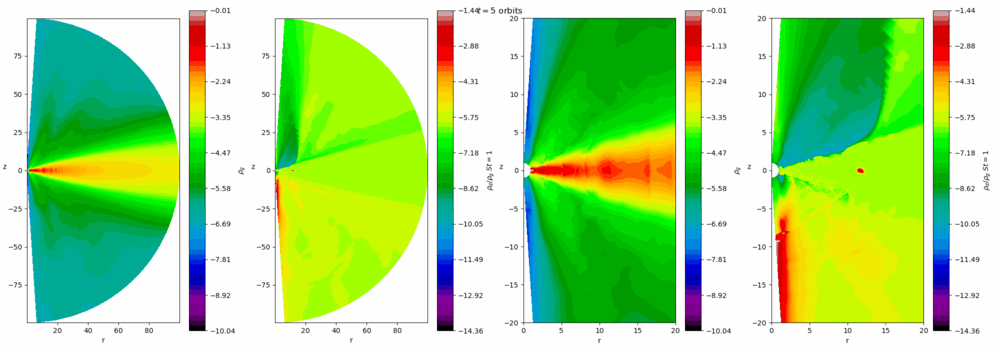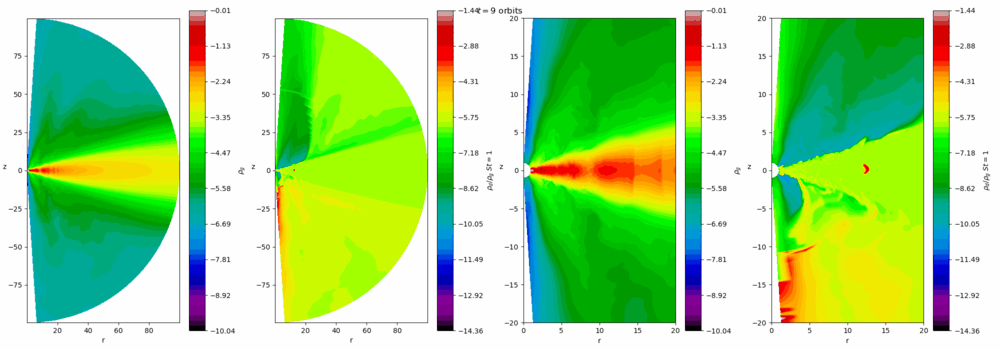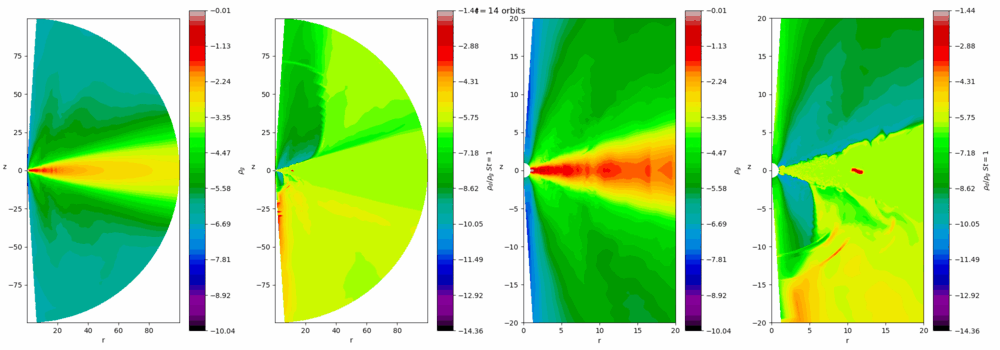
Our group is interested in the turbulence that prevails in these discs and the instabilities that sustain them. Turbulence helps the discs accrete, and also influences the process of planet formation in protostellar discs. The magnetorotational instability (MRI) is the main cause of activity in well-ionised discs, such as dwarf novae, X-ray binaries, and active galactic nuclei. In more massive colder discs, such as young protostellar discs, gravitational instability (GI) is the leading cause. At certain times and locations both instabilities or neither occur, leading to rich and violent dynamics, such as FU Orionis or EX Lupi outbursts which occur on timescales of 100-1000 years. On the other hand, the interplay between the MRI and thermal instability leads to cycles of repeated outbursts on much shorter timescales (days and weeks) in dwarf novae that amateur astronomers can observe. Our group uses numerical simulations (and analytical techniques when possible) to better understand these complicated processes.

Other topics that we work on include (but are not limited to) (a) the powerful outflows and jets that are launched from almost all discs at certain times of their evolution, (b) how discs become warped and eccentric and what sustains these non-circular geometries, (c) large-scale waves and oscillations in discs around black holes and neutron stars, and the signatures of general relativity upon them, (d) dust dynamics, vortices and dust-gas instabilities in planet formation, and (e) patterns and structures in Saturn's rings.
Planet–disc interactions
Solid material embedded in a gas disc is subject to radial migration. Small particles (up to a few 100 km in size) are subject to aerodynamic drag, causing them to migrate inward on time scales that can be alarmingly fast (100 years for metre-sized objects).
Earth-like planets are massive enough to excite tidal sound waves in the disc, one inside its orbit and one outside. These are of unequal strength in general, mainly due to the nonlinear nature of Keplerian rotation (the rotation profile is asymmetric with respect to the orbit of the planet). This leads to a torque on the planet, that usually corresponds to inward migration called Type I migration. For super-Earth planets (and also possibly the cores of giant planets) the time-scale for inward migration can be as short as 105 years. This has to be compared to a disc lifetime of 107 years, implying that essentially there should be no planets at large distances (1–10 au) from the central star! This is a serious problem, and possible solutions include MHD turbulence and non-linear effects on the corotation torque, especially in non-barotropic discs.
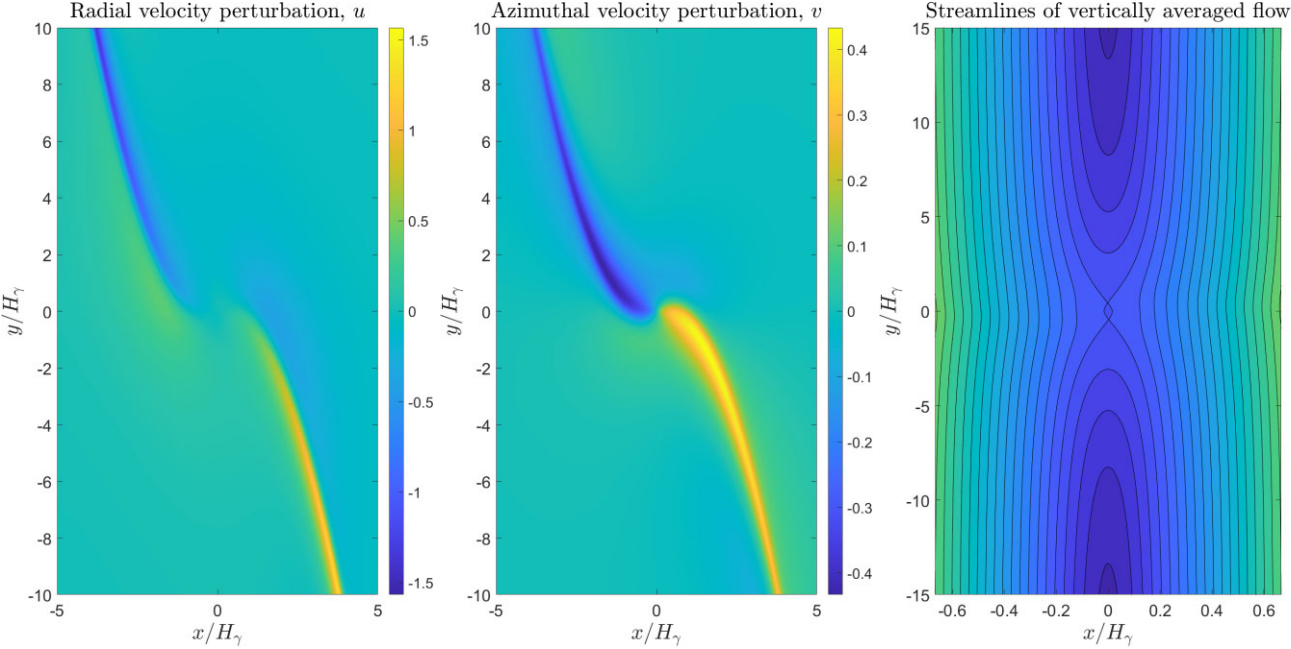
Massive planets, comparable to Jupiter, excite nonlinear waves in the disc, leading to the formation of an annular gap (see movie below). The migration of the planet slows down considerably, and is now called Type II migration. Basically, in this regime the planet just accretes with the gas onto the star, making the migration time scale comparable to the disc life time.
For intermediate masses, comparable to Saturn, rapid Type III migration can occur. This mode of migration is driven by a strong coorbital flow, and can in principle be directed either inward or outward. This is a very challenging problem, numerically, because it relies on the flow in the direct vicinity of the planet which is difficult to treat in a realistic way.
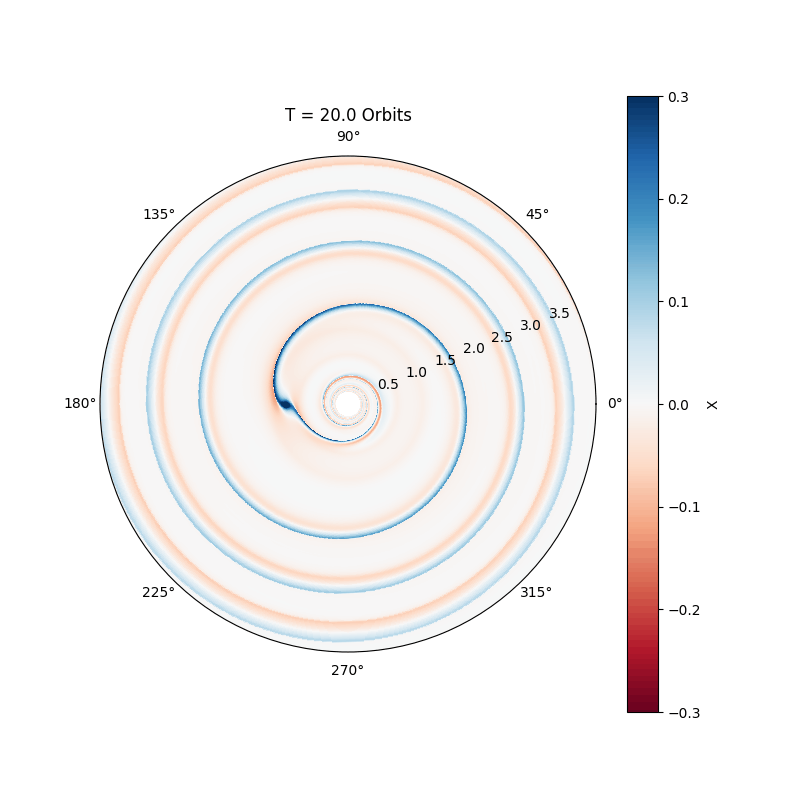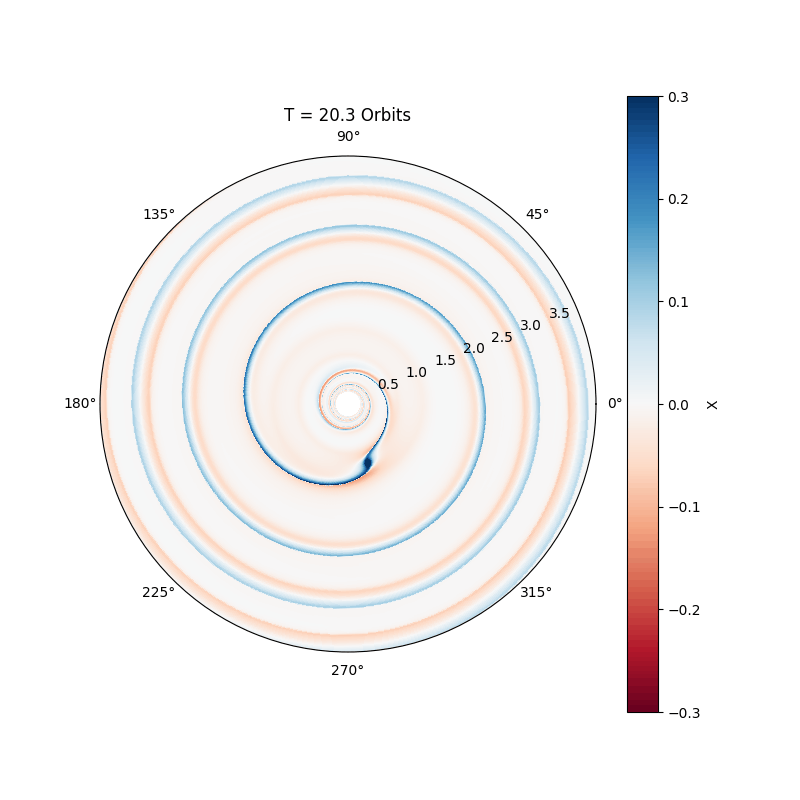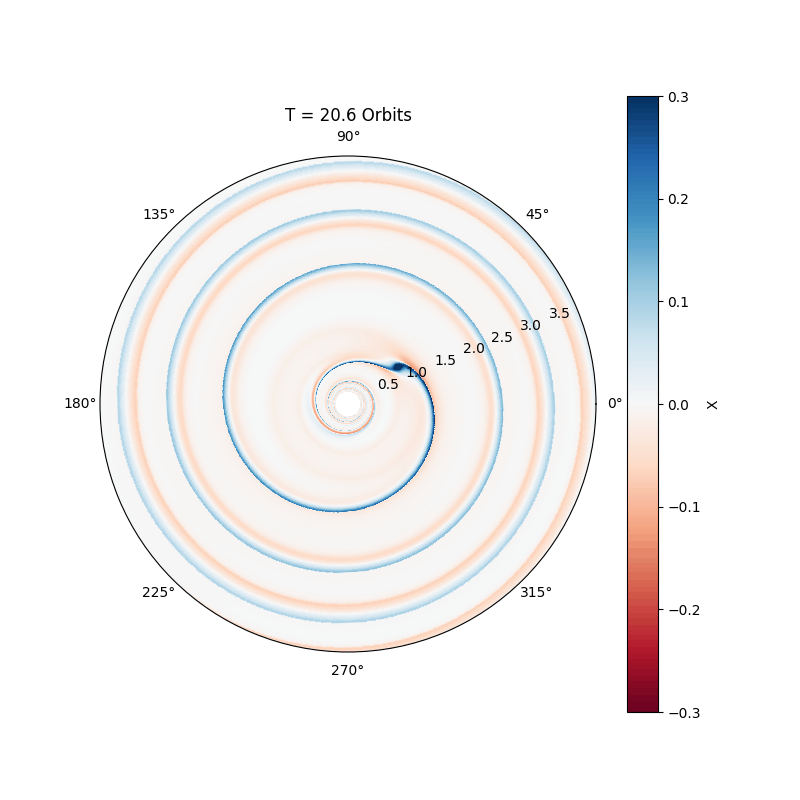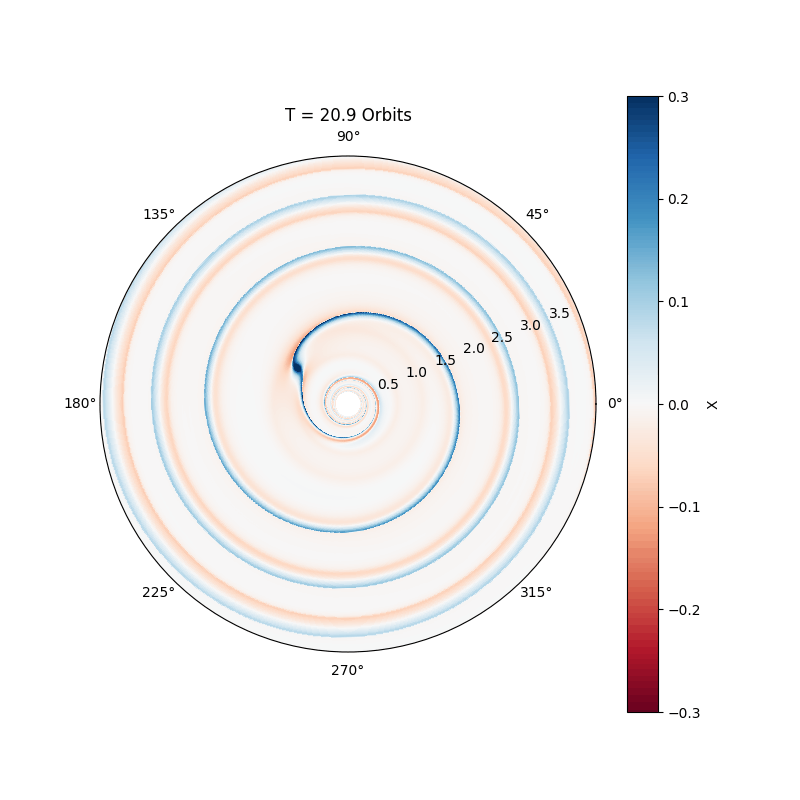
Planet formation in binary systems
Making planets is difficult in general, and it is even more difficult in systems that have an additional strong perturber in the form of a companion star. Nevertheless, a planet has been found at 2 au around a star that has a companion of 0.5 M_Sun at only 20 au (orbital distance of Uranus!). Moreover, this massive companion in on a very eccentric orbit. The strong gravitational perturbations due to this second star puts planets-to-be in all sorts of trouble. One fundamental problem arises when you try to grow a population of km-sized planetesimals into larger bodies that will eventually accrete gas to form a giant planet. The perturbations of the secondary star excites the eccentricities of the planetesimals. This leads to very high encounter velocities (up to 1 km/s), which makes collisions between planetesimals very violent and destructive. The presence of a gas disc to damp the eccentricities of the planetesimals does not help. Since the strength of gas drag is size-dependent, planetesimals of different size will still be on very different orbits. This so-called differential orbital phasing leads again to very violent collisions between bodies of unequal size. It is difficult to see how to overcome this problem and proceed with building bigger bodies.
